Knowledge Tracing과 그를 위한 Attention mechanism에 대한 지식이 없으시다면, 아래의 Riiid Teamblog 글을 읽고 오시길 추천합니다:

• Deep Knowledge Tracing
• Attention Mechanism for Knowledge Tracing

문제 제기

먼저 AKT는 기존의 논문들(특히, DKT 계열: SAKT, DKVMN등)이 제대로 반영하지 못한 세 가지 학습 특성을 지적하고 있습니다

1. Concept도 중요하지만, 개별 Problem간의 차이도 중요하다.

원문: questions labeled as covering the same concept are closely related but have important individual differences that should not be ignored.

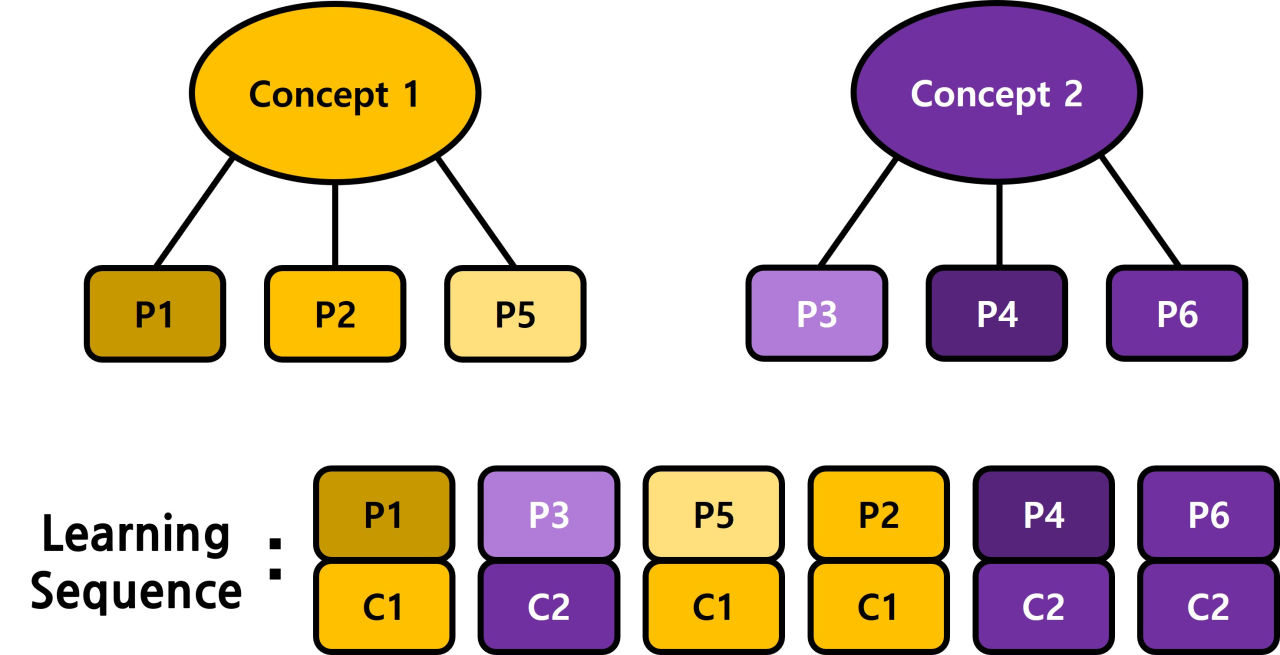
위의 그림과 같이, 같은 concept에 속한 problem들은 대략적으로 비슷한 성질을 가지고 있습니다. 그러나, 각 문제마다의 차이도 분명히 존재합니다.

현재 Deep KT 모델의 대부분은 문제 개별의 차이를 무시하고 그 문제가 속한 Concept(skill) 정보만을 활용하고 있습니다. 그림의 learning sequence에서 아랫쪽 \(< C_1,C_2,C_1,C_1, ...>\)처럼 문제 각각의 특성이 반영되지 않은 input만을 사용하고 있는 것입니다.

기존 모델이 이렇게 된 이유는 크게 두 가지가 있습니다.

첫 번째로, Problem의 갯수 \(Q\)의 크기가 Concept의 갯수 \(C\)보다 매우 크기 때문에(\(Q >> C\)) 각각의 문제 모두를 Embedding하면 Embedding 크기만 \(Q·D\) (\(D=(embedding\_dim)\))가 되어 메모리 효율이 극도록 하락하기 때문이고,

두 번째로, 각 concept은 그 concept을 학습한 사람이 많아 학습하기에 데이터가 충분하지만, 각 Problem을 학습한 인원은 그보다 훨씬 적어 Data Sparsity 문제가 발생하기 때문입니다.

2. 같은 문제를 보더라도 사람마다 받아들이는 방식이 다르다

원문: the way a learner comprehends and learns while responding to a question depends on the learner.

당연하지만, 모든 학생은 자신의 경험을 토대로 당면한 문제를 풀고, 또 정보를 받아들입니다. 다시 말해, 같은 문제라도 각각의 학생마다 받아들이는 방식(i.e. embedding vector)가 달라질 수 있다는 것입니다.

그러나 현재의 Deep KT관련 모델은 이러한 사실을 잘 반영하지 않은 채, 단순히 각 concept마다의 embedding을 사용하고 있으므로, 학생 각각의 특성을 잘 반영하지 못한다고 할 수 있습니다.

3. 오래 전에 푼 문제는 잊혀지고, 현재 풀고 있는 문제과 관련 없는 지식은 사용되지 않는다

원문: when a learner faces a new question, past experiences i) on unrelated concepts and ii) that are from too long ago are not likely to be highly relevant.

예를 들어, 어떤 모델 \(M\)이 학생 \(S\)가 어떤 문제 \(q_t\)를 풀 수 있을 지 예측하기 위해 앞의 200문제 (\(q_{t-200}, ... , q_{t-1}\))를 살펴본다고 합시다. 현재 대부분의 Attention 기반 Deep KT 모델은 여기서 \(q_{t-200}\)과 \(q_{t-1}\)을 동등하게 사용하고 있습니다. 그러나 이것은 학생이 이전에 푼 문제를 점점 잊는다는 사실을 무시한 것입니다. 학생이 \(q_{t-200}\)에 관해 기억하고 있는 정보의 양과 \(q_{t-1}\)에 관해 기억하고 있는 정보의 양은 다를 수밖에 없고, 이러한 사실이 모델에 반영되면 좋은 효과를 기대할 수 있을 것입니다.

또 하나, 학생이 “Venn Diagram” Concept을 학습하다가, 잠시 “Prime Number”에 관한 숙제를 하고, 다시 “Venn Diagram”을 학습하게 되었다고 가정해 봅시다. 이 경우, 학생이 최근에 풀었던 “Prime Number” 정보보다는 그 전에 학습했던 “Venn Diagram”관련 문제 정보가 훨씬 중요할 것입니다. 이런 식의 concept switching은 생각보다 자주 일어나는 일이지만, 아직까지 이를 명시적으로 고려한 모델은 없습니다.

Contribution

AKT에서는 위에서 주장한 주요 문제점을 해결하기 위해 다음의 세 가지 contribution을 만들었다고 주장합니다:

1. Rasch Model-Based Embeddings

“Concept도 중요하지만, 개별 Problem간의 차이도 중요하다.”

Rasch model에서 영감을 받아, AKT는 Problem 각각의 차이를 반영하면서도 메모리 사용량과 Data Sparsity 문제를 효과적으로 해결할 수 있는 Problem Embedding 기법을 도입하였습니다.

먼저, timestamp \(t\)에서 question \(q_t\) of concept \(c_t\)의 embedding \(x_t\)는 다음과 같이 정의됩니다:

여기에서 \(\textbf{c}_{c_t} \in \mathbb{R}^D\)는 \(c_t\)의 base embedding, \(\mu _{q_t} \in \mathbb{R}^1\)는 \(c_t\) 내에서의 \(q_t\)의 난이도를 나타낸 하나의 숫자, \(\textbf{d}_{c_t} \in \mathbb{R}\)는 개별 Problem의 난이도에 따른 embedding varition을 나타내는 벡터입니다.

이러한 방식으로 임베딩을 할 경우, 앞서 언급했더 Problem을 Embedding하는 것이 어려운 이유 두 가지를 효과적으로 회피할 수 있습니다.

• 메모리 부족 문제

Problem의 갯수를 \(Q\), Concept의 갯수를 \(C\), 각 Embedding의 Dimension을 \(D\)라고 했을 때, 단순히 Problem각각을 Embedding하면 \(QD\)의 메모리가 소모됩니다. 하지만 위 방식은 \(2CD+Q\) (\(CD\) for \(\textbf{c}, \textbf{d}\), \(Q\) for \(\mu\))만큼 메모리를 소모하므로, \(Q >> C\)임을 감안하면 메모리가 크게 절약됩니다.

비슷하게, 학생이 어떤 문제 \(q_t\) 를 맞히거나 틀렸을 때(\(r_t\)) 얻는 정보를 나타내는 벡터 \(y_t\)(knowledge embedding)은 다음과 같이 정의됩니다:

위와 마찬가지로, \(\textbf{e}_{c_t,r_t} \in \mathbb{R}^D\), \(\textbf{f}_{c_t,r_t} \in \mathbb{R}^D\)는 각각 base knowledge embedding, Problem 난이도에 따른 embedding variation을 나타냅니다.

추가적으로, knowledge embedding에서는 메모리 효율을 위해 \(\textbf{e}_{c_t,r_t}\)를 앞에서 구한 \(\textbf{c}_{c_t}\)를 이용해 재정의하였습니다. 위의 식에서, \(r_t \in \{0,1\}\)이므로, \(\textbf{g}_{r_t}\)는 \(2D\)만의 메모리(negligible)를 소모합니다.

• Data Sparsity

Problem 개별의 Embedding이라고는 해도, 기본적으로 concept embedding \(c_{c_t}\)에서 출발하기 때문에 Problem embedding을 처음부터 학습하는 것보다 훨씬 효율적입니다.

2. Context-aware Representations of question and knowledge

같은 문제를 보더라도 사람마다 받아들이는 방식이 다르다

각각의 problem embedding과 knowledge embedding이, 학생이 이전에 풀었던 problem에 영향을 받도록 하여 학생 개개인에 맞춘 embedding을 생성하였습니다. 다시 말해, 학생 개인에 맞춘 problem embedding \(\textbf{x}\prime_{t} = \textit{f}_{enc} (\textbf{x}_1, \textbf{x}_2, ..., \textbf{x}_t)\)로 정의하였습니다. 여기에서, AKT는 \(f_{enc_x}\)로 self-attention mechanism을 사용하였습니다.

추가로, knowledge embedding, \(\textbf{y}_t\)에 대해서도 같은 작업을 진행하였습니다.

3. monotonic attention mechanism

오래 전에 푼 문제는 잊혀지고, 현재 풀고 있는 문제과 관련 없는 지식은 사용되지 않는다

기존의 attention에서 attention weight \(\alpha_{t,\tau}\)는 다음과 같이 정의됩니다:

monotonic attention에서는 attention weight가 다음과 같이 정의됩니다:

\(\theta > 0\)는 learnable decay parameter, \(d(t,\tau)\)는 각 timestamp \(t,\tau\)간의 거리 함수입니다.

여기서 두 timestamp간의 거리 함수 \(d(t,\tau)\)는 1) 오래 전에 푼 문제를 잊는 것과 2) 현재 풀고 있는 문제와 관련 있는 지식만 골라내는 역할을 합니다.

거리 함수는 다음과 같이 구성되어 있으며:

여기서 앞의 \(t-\tau\) 는 오래 된 지식을 잊게 하는 역할을 하고, 뒤의 \(\sum_{t'=\tau+1}^{t} f_{attn}(t,t')\)는 attention weight를 통해 문제와 관련 없는 지식을 걸러내는 역할을 합니다.

모델 구조

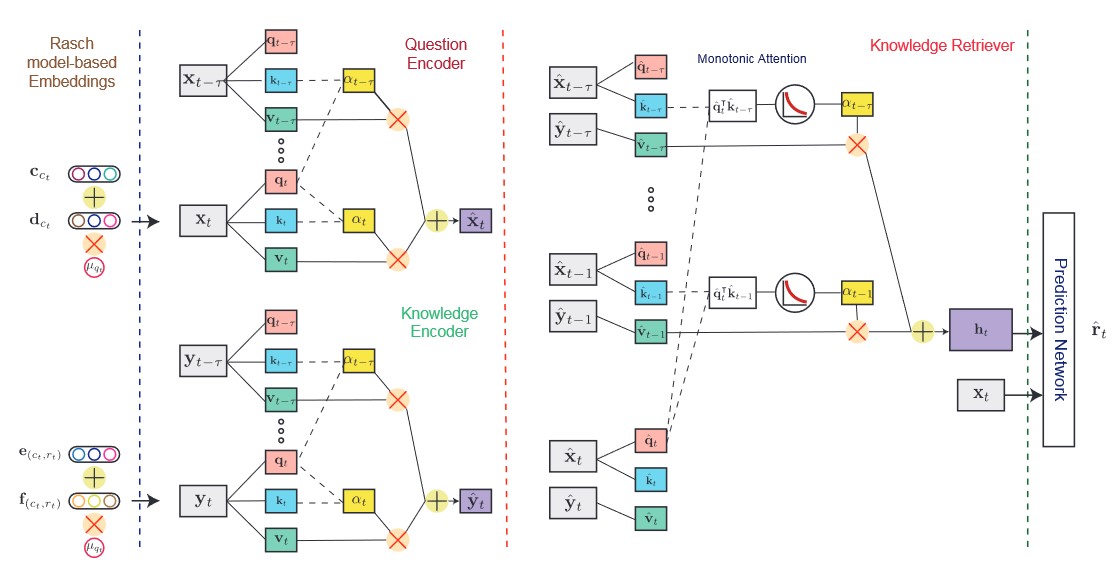
최종적인 모델 구조는 위 그림과 같습니다. Input sequence가 들어오면,

1. 먼저 Rasch model-based embedding을 만들고,

2. Attention 기반의 question encoder와 knowledge encoder로 context-aware representation을 만들고,

3. 생성된 Context-aware embedding을 이용하여 예측을 수행합니다.

2.와 3.에 사용되는 모든 attention은 motonic attention mechanism을 사용합니다.

구현

구현 과정

1. 논문을 보고 대략적으로 모델 구현

2. official repo를 참고하여 각종 parameter값을 넣고, 실수한 부분이나 논문과 코드가 다른 부분을 대략적으로 수정 (models/akt.py, BaseAKTEstimator)

3. official repo를 참고하여 코드 한두 줄로 끝나지 않을 만한 큰 변화들을 반영 (models/originalakt.py, OriginalAKTEstimator)

• 데이터셋의 경우, 원활한 비교를 위해 official code와 최대한 똑같은 데이터를 내도록 하였습니다. 예를 들어 데이터를 length=200으로 자르는 과정에서 자르는 위치를 달리하여 data augmentation을 할 수도 있으나, official code가 그러고 있지 않은 것으로 보이므로 data augmentation을 하지 않았습니다.

구현 결과

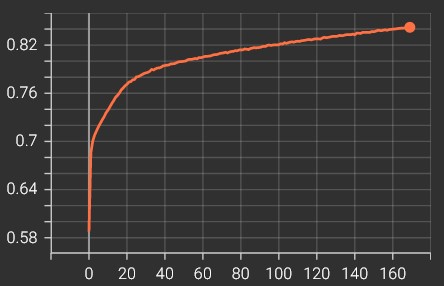
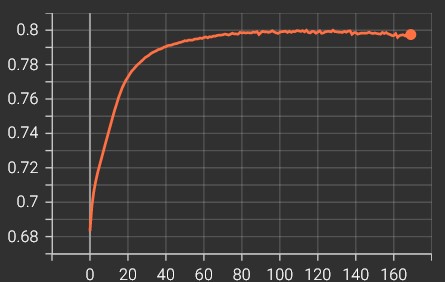
Training Curve

• training auc

• validation auc

최종 결과

mean AUC on 5 folds: 0.7987
mean accuracy on 5 folds: 76.01%

why lower?

• motonic attention의 경우, official coda와 이 프로젝트의 output이 거의 같음을 확인함 (cuda version 차이 등에서 오는 작은 변화 제외)

np.random.seed(224)
query = torch.from_numpy(np.random.normal(0.7,1.3,query.shape)).type(query.dtype).to(query.device)
key = query.clone().detach()
value = torch.from_numpy(np.random.normal(1.2,1.9,query.shape)).type(query.dtype).to(query.device)
torch.nn.init.constant_(self.decay_rate,0.27)
attended_features = self.monotonic_attention(query,key,value,mask)

위와 같은 input(akt.py,L727)을 이 프로젝트 attention에 넣었을 때,

torch.std(attended_features) # = 1.9523
print(attended_features[0,3,77])
# tensor([ 1.8664, -0.5779, -0.0891, -2.5754,  0.6524,  1.7813,  2.0745,  0.9368,
#          0.2846,  0.6477,  3.7393,  0.8715,  1.2119,  0.4349, -1.8076,  2.2776,
#          1.4826,  1.8024,  2.4675,  3.2923,  1.6706, -2.1705, -0.6615,  0.5187,
#          0.6413,  2.2926, -0.5753,  5.9830,  1.8191, -0.1177,  1.3508,  2.1476],
#       device='cuda:0', grad_fn=<SelectBackward0>)

위와 같은 결과가 나옴.

AKT official code의 경우,

np.random.seed(224)
q = torch.from_numpy(np.random.normal(0.7,1.3,q.shape)).type(q.dtype).to(q.device)
k = q.clone().detach()
v = torch.from_numpy(np.random.normal(1.2,1.9,q.shape)).type(q.dtype).to(q.device)
torch.nn.init.constant_(self.gammas,0.27)
scores = attention(q, k, v, self.d_k,
                    mask, self.dropout, zero_pad, gammas)

위 코드로 테스트하였음(akt.py). 결과는,

torch.std(scores) # = 1.9521
print(attended_features[0,3,77])
# tensor([ 1.8664, -0.5780, -0.0891, -2.5754,  0.6524,  1.7813,  2.0745,  0.9368,
#         0.2846,  0.6477,  3.7393,  0.8715,  1.2119,  0.4348, -1.8076,  2.2776,
#         1.4826,  1.8024,  2.4675,  3.2923,  1.6706, -2.1706, -0.6615,  0.5187,
#         0.6413,  2.2926, -0.5753,  5.9830,  1.8190, -0.1177,  1.3508,  2.1475],
#       device='cuda:0', grad_fn=<SelectBackward>)

위와 같음.

• 위의 결과로 볼 때, gpu arch의 차이나 pytorch version up에 따른 차이가 있을 수 있음
• 논문에서 나오지 않아 구현되지 않았거나, 차이가 나는 부분이 조금 더 존재하는 것으로 보임
• fold 1에서 official code를 돌렸을 때, seed 값을 디폴트에서 바꾸면(seed=772) auc=0.819 수준의 결과가 나옴을 확인함. 이것도 영향이 있을 것으로 보임

ROC Curve

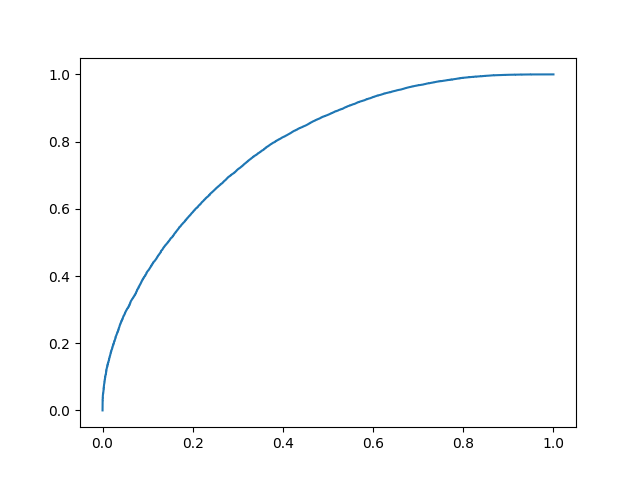
후기

의문스러웠던 것들

저자인 Aritra Ghosh가 공개한 official code를 살펴본 결과, 실제 코드가 논문과 다르게 구현되었거나, 혹은 논문에 설명되지 않은 것이 코드에는 들어 있는 경우가 많았습니다. 또, official code의 구현 중 의문스러운 것들도 있었습니다.

아래는 그것들 중 기억나는 것을 모아 본 것입니다

K-Fold Cross validation

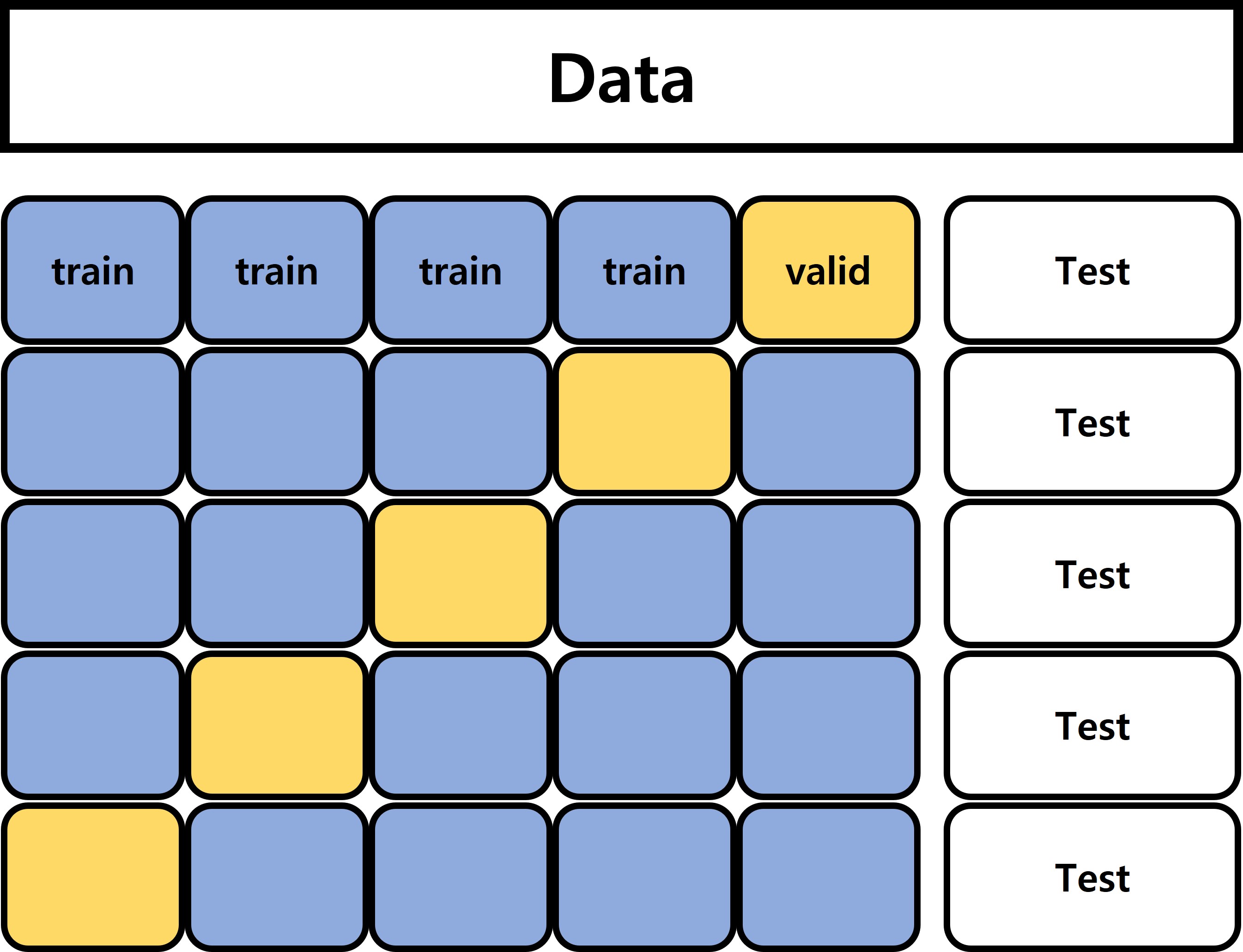
위 그림과 같이, 일반적으로 K-Fold cross validation은 먼저 TEST set을 따로 빼 놓고 나머지를 K등분 하여 train/valid로 사용, 최종적으로 학습된 5개의 모델을 종합하여 Test 결과를 얻는 방식을 말합니다.

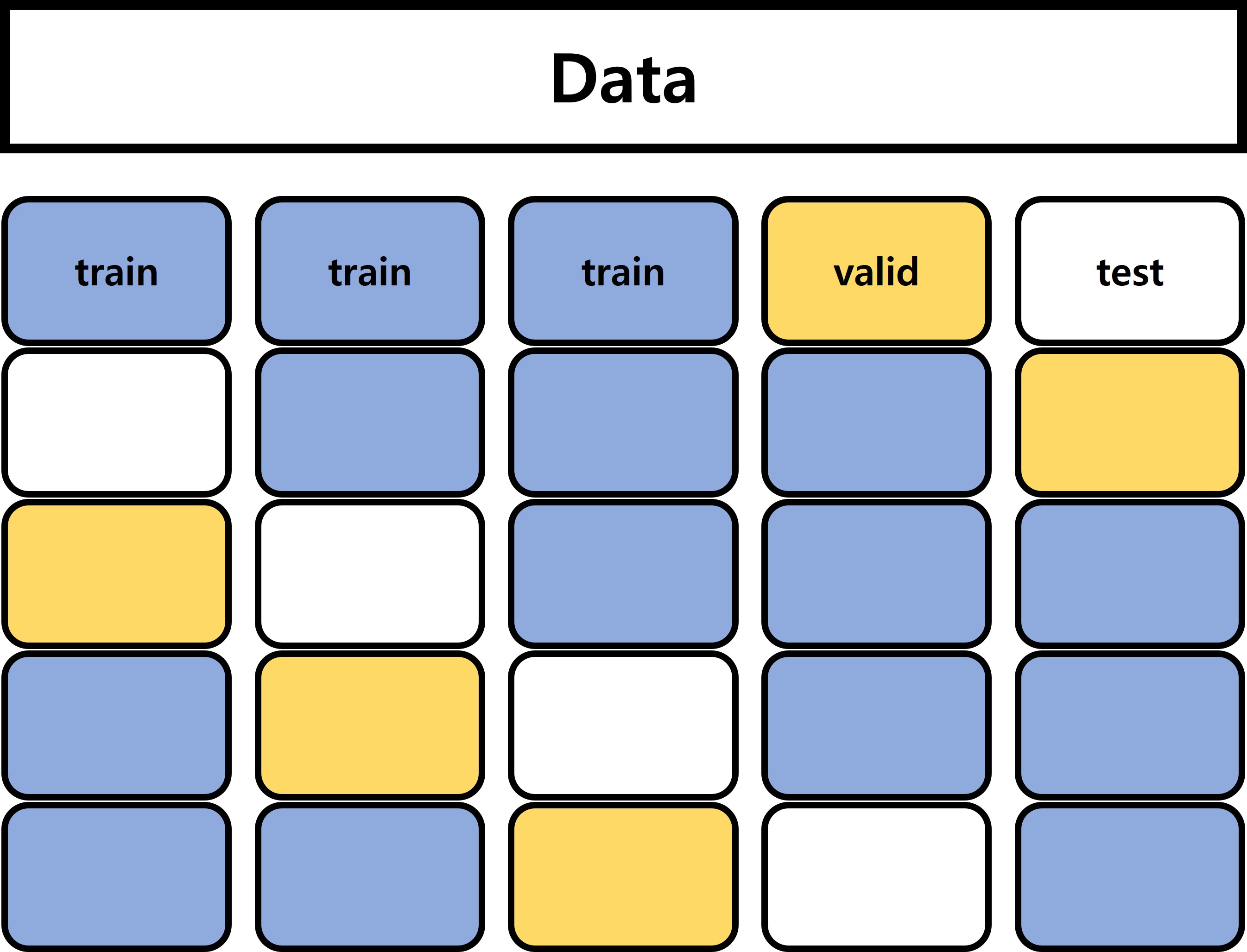
그러나 이 논문에서 사용한 방법은 조금 다릅니다. 위 그림과 같이, 여기서는 전체 데이터를 K등분 한 뒤 train/valid/test를 돌려 가며 테스트하고 있습니다. 이렇게 할 경우, 생성된 5개의 모델 중 누군가는 다른 모델의 Test set을 학습하게 되므로, 5개의 모델을 종합하여 쓸 수도 없게 됩니다.

Attention

AKT에서는 Attention mechanism이 상당히 광범위하게 사용됩니다. Context-Aware Feature Encoding의 Question Encoder, Knowledge Encoder 두 부분에서는 Self-attention을 사용하고 있고, Knowledge Retriever 에서는 Question embedding, knowledge embedding 둘을 섞는데 Attention Mechanism을 이용하고 있습니다.

Attention mechanism에서, query, key, value가 들어오면 이들 각각에 linear layer를 적용합니다.

k = self.k_linear(k).view(bs, -1, self.h, self.d_k)
q = self.q_linear(q).view(bs, -1, self.h, self.d_k)
v = self.v_linear(v).view(bs, -1, self.h, self.d_k)
... (do attention on k,q,v)

그러나, 실제 구현된 코드를 보면 AKT에 사용된 Attention이 일반적인 Attention과는 조금 다른 것을 확인할 수 있습니다.

k = self.k_linear(k).view(bs, -1, self.h, self.d_k)
q = self.k_linear(q).view(bs, -1, self.h, self.d_k)     # self.k_linear applied on q
v = self.v_linear(v).view(bs, -1, self.h, self.d_k)
... (do attention on k,q,v)

(본래 코드는 이것과 약간 다르나, 항상 “True”인 한 parameter를 제외하면 위와 같아집니다)

일반적으로 Attention은 input key와 query가 같더라도 이들에게 적용되는 linear layer가 다르나, 여기서는 둘을 똑같은 것으로 사용합니다.

Rasch Model-Based Embeddings

위에서, 학생이 어떤 문제 \(q_t\) 를 맞히거나 틀렸을 때(\(r_t\)) 얻는 정보를 나타내는 벡터 \(y_t\)(knowledge embedding)은 다음과 같이 정의된다고 하였습니다:

그러나 실제로 코드를 보면 \(\textbf{f}_{c_t,r_t}\) 또한 이와 같은 방식의 embedding을 사용하고 있었습니다:

논문의 context상 이해가 되지 않는 선택은 아니나, 한 줄이라도 써 주었으면 어떨까 합니다.

Monotonic Attention

monotonic attention에서 attention weight를 구하는 식은 다음과 같았습니다:

그러나, 실제로는 다음과 같이 구해지고 있었습니다:

References

• Ghosh, Aritra and Heffernan, Neil and Lan, Andrew S, “Context-Aware Attentive Knowledge Tracing”, In KDD, 2020.
• Ghosh’s official AKT code: https://github.com/arghosh/AKT
• Riiid Teamblog, “학습 시점과 문항 유사도를 고려한 Knowledge Tracing 모델”: https://medium.com/riiid-teamblog-kr/%ED%95%99%EC%8A%B5-%EC%8B%9C%EC%A0%90%EA%B3%BC-%EB%AC%B8%ED%95%AD-%EC%9C%A0%EC%82%AC%EB%8F%84%EB%A5%BC-%EA%B3%A0%EB%A0%A4%ED%95%9C-knowledge-tracing-%EB%AA%A8%EB%8D%B8-5192a3e28f46

2023-01-11 13:00